↓메인 콘텐츠로 이동하기

DiffUtil의 핵심 알고리즘, Myers's Difference Algorithm 알아보기

·11 분
Algorithm Android
cover
Image generated by Gemini
목차

Compose 이전에는 안드로이드에서 대량의 정보를 UI에 보여주기 위해서는 RecyclerView를 사용했다. 또한 많은 개발자들이 편리하게 변경점을 업데이트 하기 위해서 DiffUtil을 함께 사용했다. DiffUtil 덕분에 많은 개발자들이 변경 사항을 하나 하나 업데이트 해주어야 했던 번거로움에서 해방되었다.

Compose가 주력으로 자리잡은 지금은 LazyList를 통해서 대량의 정보를 UI에 표현한다. Compose가 선언적 UI 패러다임을 따르는 프레임워크인 만큼 LazyList는 RecyclerView처럼 별도로 변경 사항을 알리지 않아도 자동으로 UI에 반영된다.

자동으로 처리해 준다고 하지만 Compose도 마법은 아니다. Compose 내부에는 이전 상태와 최신 상태를 비교하고 변경점을 찾아서 최소한의 변경으로 업데이트 해야 할 부분을 찾는 동작이 숨어 있다. Compose의 비교 알고리즘이 DiffUtil의 것과 같지는 않지만, DiffUtil이 areItemsTheSame 메서드를 통해 아이템의 고유성을 판단한 것 처럼 LazyList에 전달하는 key로 아이템의 고유성을 판단하는 원리는 맞닿아 있다. 즉, DiffUtil의 원리를 파악한다는 것은 LazyList를 사용하면서 key를 사용하는 이유를 이해하는데에도 도움이 된다. 또한 안드로이드 분야를 넘어 “무엇이 바뀌었는지"를 찾는 Diff 알고리즘을 이해하는 것은 컴퓨터 과학 지식을 넓히는 데에도 도움이 된다.

단순히 예전의 기술을 돌아보는 것이 아니라 Compose 이전에 안드로이드 생태계를 지탱해온 DiffUtil을 깊게 파헤쳐보고 앞으로 UI 패러다임이 변해도 흔들리지 않을 기반 지식을 얻어가보고자 한다.

Myers’s Difference Algorithm #

DiffUtil의 차이점 비교 알고리즘은 유진 마이어스(Eugene W. Myers)가 1986년에 발표한 Difference Algorithm에 기반한다. Myers’s Difference Algorithm을 사용하면 두 리스트 간의 최소 편집을 통해 똑같이 만드는 방법을 알 수 있다. 단, 이 알고리즘으로는 “추가”, “삭제”, “유지” 총 3가지 동작만 알 수 있어서 DiffUtil은 여기에 “이동” 동작을 추가한 변형을 사용한다.

Myers’s Difference Algorithm의 개념 #

Myers’s Difference Algorithm은 두 개의 시퀀스1 사이의 최소 편집 스크립트(Shortest Edit Script, SES)2를 찾아내는 알고리즘이다.

DiffUtil에서 시퀀스는 RecyclerView가 가진 데이터 리스트가 될 것이다. 즉, DiffUtil 내부의 Myers’s Difference Algorithm은 이전 리스트에서 새로운 리스트로 업데이트 할 때 얼마나 적은 명령으로 가능한지 구하는 역할을 한다.

그렇다면 Myers’s Difference Algorithm는 어떻게 동작할까?

Myers’s Difference Algorithm은 두 개의 시퀀스를 2차원 격자로 모델링한다. X축은 이전 시퀀스, Y축은 신규 시퀀스를 나타낸다. 알고리즘은 격자의 시작점\((0, 0)\)에서 끝점\((n, m)\)까지 가는 경로를 탐색한다. 이 때, 경로 이동에 따라서 편집 필요성이 결정된다.

  • 가로 이동: 이전 시퀀스에서 아이템이 삭제됨. 편집 필요.
  • 세로 이동: 신규 시퀀스에 아이템이 추가됨. 편집 필요.
  • 대각선 이동: 두 시퀀스 사이에 아이템이 동일함. 편집 불필요.

알고리즘의 목표는 격자의 시작점에서 끝점까지 이동하는 경로 중 가장 편집 횟수가 적은 경로를 찾는 것이다.

예를 들어 [A, B, C, D]시퀀스를 [A, C, E]시퀀스로 바꾸는 최소 편집 스크립트를 구해 본다고 하자. 우선 두 시퀀스를 기반으로 2차원 격자를 모델링해보자.

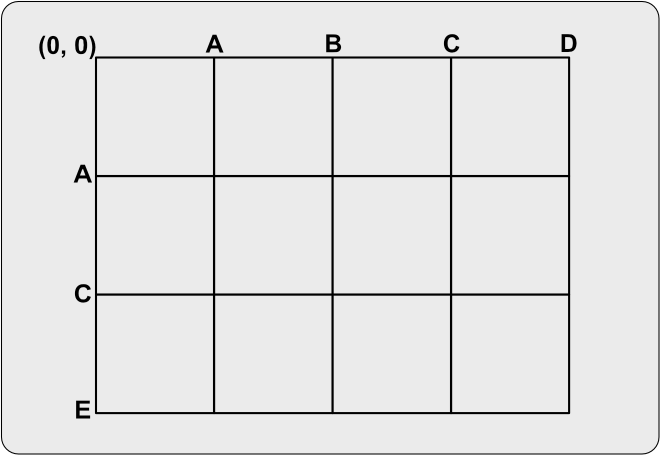
table

X축에는 이전 시퀀스를, Y축에는 신규 시퀀스에 따라 2차원 격자를 만들었다. 이제 격자의 시작점에서 끝점까지 이동하며 편집 횟수가 가장 적은 경로를 찾아야 한다.

  1. 이전 시퀀스의 첫 아이템은 A고 신규 시퀀스의 첫 아이템도 A다. 두 시퀀스의 아이템이 같으므로 편집이 필요 없다. 따라서 대각선으로 이동해 \((1, 1)\)로 간다.

  2. 이전 시퀀스의 다음 아이템은 B이고 신규 시퀀스의 다음 아이템은 C다. 두 아이템은 다르다. 이 때, 가로로 이동할지 세로로 이동할지 정해야 하는데 Myers’s Difference Algorithm은 가중치(편집 비용)가 있는 너비 우선 탐색(Breadth First Search)을 통해서 최단 거리를 찾는다. \((1, 1)\)에서 최단 거리로 끝점까지 가려면 가로로 이동해야 하니 \((2, 1)\)로 이동한다.

  3. 가로로 이동했으니 이전 시퀀스는 다음 아이템을 보아야 하고 다음 아이템은 C다. 세로로는 이동하지 않았으니 신규 시퀀스는 그대로 C다. 두 아이템이 같으니 대각선으로 이동해 \((3, 2)\)로 간다.

  4. 이전 시퀀스의 아이템은 D, 신규 시퀀스의 아이템은 E다. 두 아이템이 다르고 최단 거리로 이동해야 하므로 가로로 이동해 \((4, 2)\)로 간다.

  5. 이전 시퀀스의 아이템은 모두 소진했으니 신규 시퀀스의 아이템을 추가해야 한다. 세로로 이동해 끝점인 \((4, 3)\)으로 긴다.

끝점에 도달했으니 지나온 경로를 확인해보면 다음과 같다.

path

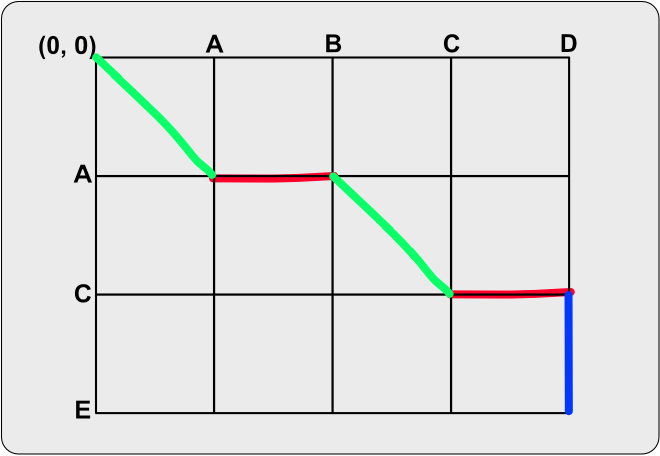
결과를 정리하자면 다음과 같다.

  • A: 유지
  • B: 삭제
  • C: 유지
  • D: 삭제
  • E: 추가

정리하자면, [A, B, C, D]시퀀스를 [A, C, D]시퀀스로 변환하는 최소 편집 스크립트(SES)는 B와 D 삭제, E 추가다.

Myeres’s Difference Algorithm의 구현 #

Myers’s Difference Algorithm을 실제 코드로 구현해보자.

우선 알고리즘 진행 중 상태를 저장 할 준비물을 구현한다. 준비물은 두 가지다.

  • 최단 경로 스크립트에 저장 할 각각의 편집 작업.
  • 알고리즘 진행 중 이동 경로를 저장할 그릇.
/**
 * 최단 경로 스크립트에 저장 할 각 편집 작업.
 */
sealed class DiffOp {
    /** 변경 없음 */
    data class Keep(val item: String) : DiffOp()
    /** 추가됨 */
    data class Insert(val item: String) : DiffOp()
    /** 삭제됨 */
    data class Delete(val item: String) : DiffOp()
}

/**
 * 이동한 경로를 저장하기 위한 객체. 각 지점의 발자국.
 *
 * 모든 경로 탐색 후 각 단계에서 어떻게 이동했는지 역추적하기 위해서 경로를 저장함.
 * 각각의 PrevNode 객체는 경로 중 이동한 위치에 대한 정보를 담으며, 이전 위치를
 * 저장해 거꾸로 추적 가능하도록 설계.
 *
 * @param x 현재 위치의 X좌표.
 * @param y 현재 위치의 Y좌표.
 * @param prev 현재 위치로 오기 전의 위치.
 */
private data class PathNode(
    val x: Int,
    val y: Int,
    val prev: PathNode?,
)

이제 핵심 알고리즘을 구현한다.

두 개의 리스트를 받고, 편집 스크립트(List<DiffOp>)를 반환하는 함수를 작성해야 한다.

알고리즘은 2개의 리스트의 길이만큼의 가로, 세로 길이를 가진 가상의 2차원 격자 위에서 최단 경로를 찾아야 한다. 최단 경로 탐색은 편집 비용을 가중치로 사용하는 너비 우선 탐색(Breadth First Search)를 기반으로 한다. 편집 비용은 변경이 없을 때는 0, 추가 또는 삭제 시 1로 한다.

또한 최단 경로를 찾았을 때, 지금까지 지나 온 경로를 되돌아보면서 최단 편집 스크립트를 만들어야 하기 때문에 이동한 경로를 저장해야 한다.

이 내용을 기반해서 기본적인 알고리즘의 틀을 구현하면 아래와 같다.

fun calculateDiff(
    old: List<String>,
    new: List<String>,
): List<DiffOp> {
    val n = old.size
    val m = new.size
    val max = n + 1

    // 이동한 경로 내역.
    val history = mutableListOf<Map<Int, PathNode>>()

    for (...) {
        // 편집 비용을 가중치로 사용하는 너비 우선 탐색.
    }

    // 탐색할 것이 없으면 빈 목록 반환.
    return emptyList()
}

실제 핵심 알고리즘을 구현하기 전, Myers’s Difference Algorithm의 공간 복잡도 최적화를 이해해야 한다.

탐색을 할 때, 2차원 격자의 모든 요소를 실제 메모리에 할당하지 않아야 한다. 격자의 크기만큼 2차원 배열로 메모리를 할당받으면 지나치게 메모리 소모가 커지기 때문이다. 예를 들어 각 리스트의 아이템이 1만개만 되어도 격자는 10000 × 10000, 즉 1억개의 아이템만큼 메모리를 할당받아야 한다.

메모리 사용을 줄이기 위해서 이 알고리즘에서는 2차원 배열을 만들지 않는다. 대신 현재 탐색 중인 각 대각선 경로에서 도달한 가장 깊은 \(x\) 좌표만 기억한다.

대각선 경로란 무엇일까?

이 알고리즘 상에서 대각선 이동은 비용이 없다. 또한 가로, 세로 이동은 모두 비용이 1이다. 가로 이동을 1, 세로 이동을 -1로 표현하고 2차원 배열 위에서 모든 아이템에 현재 위치까지 오는데 필요한 비용을 저장하면 다음과 같아진다.

+ --- + --- + --- + --- +
|  0  |  1  |  2  |  3  |
+ --- + --- + --- + --- +
| -1  |  0  |  1  |  2  |
+ --- + --- + --- + --- +
| -2  | -1  |  0  |  1  |
+ --- + --- + --- + --- +
| -3  | -2  | -1  |  0  |
+ --- + --- + --- + --- +

자세히 보면 같은 대각선 위에 있는 아이템들은 값이 다르지 않다는 것을 알 수 있다. 그리고 이 값을 \(k\)라고 할 때, \(k\)는 \(x\) 좌표와 \(y\) 좌표의 차이와 같다. 이 규칙을 수식으로 정리하면 \(k = x - y\) 가 된다. 또한 \(y = x - k\) 이므로 \(k\)와 \(x\)만 알면 \(y\)는 별도로 저장할 필요 없이 바로 계산해 사용할 수 있다.

이 특징을 활용해 Myers’s Difference Algorithm은 2차원 배열을 쓰지 않고 1차원 배열 하나로 경로를 추적한다.

이 최적화를 적용한 알고리즘은 아래와 같다.

fun calculateDiff(
    old: List<String>,
    new: List<String>,
): List<DiffOp> {
    val n = old.size
    val m = new.size
    val max = n + 1

    // 이동한 경로 내역.
    val history = mutableListOf<Map<Int, PathNode>>()

    // 현재 탐색 중인 대각선 경로에서 도달한 가장 깊은 x 좌표의 모음
    // 구현 시 음수 index는 불가능하기 때문에 '-max ~ max'를 '0 ~ (2 * max)'로 보정해 사용.
    val vectors = IntArray(2 * max + 1)

    // 코드 구현 상 최초 x, y 좌표를 (0, 0)으로 보장하기 위해 설정.
    // 실제 구현 시 음수 index는 불가능하니 보정하여 max + 1 위치를 1로 사용.
    vectors[max + 1] = 0

    // 편집 비용을 가중치로 사용하는 너비 우선 탐색.
    // d = 총 편집 필요 횟수
    for (d in 0..max) {
        val currentPathHistory = mutableMapOf<Int, PathNode>()

        for (k in -d..d step 2) {
            // 음수 index는 사용할 수 없으니 양수로 보정.
            val kOffset = k + max

            var x: Int
            var route: PathNode?

            if (k == -d || (k != d && vectors[kOffset - 1] < vectors[kOffset + 1])) {
                x = vectors[kOffset + 1]
                route = history.lastOrNull()?.get(k + 1)
            } else {
                x = vectors[kOffset - 1] + 1
                route = history.lastOrNull()?.get(k - 1)
            }

            var y = x - k
            var currentPath = PathNode(x, y, route)

			// 대각선으로 이동 가능한 데까지 이동.
            while (x < n && y < m && old[x] == new[y]) {
                x++
                y++
                currentPath = PathNode(x, y, currentPath)
            }

            vectors[kOffset] = x
            currentPathHistory[k] = currentPath

            // 끝점에 도달했으면 탐색을 종료하고 지나온 경로를 역추적해 최단 편집 스크립트 반환.
            if (x >= n && y >= m) {
                return buildScript(currentNode, old, new)
            }
        }

        history.add(currentPathHistory)
    }

    // 탐색할 것이 없으면 빈 목록 반환.
    return emptyList()
}

마지막으로 끝점에 도달하면 지금까지 지나 온 발자국을 역추적해 스크립트를 만드는 함수를 작성한다.

fun buildScript(
    node: PathNode?,
    old: List<String>,
    new: List<String>,
): List<DiffOp> {
    val script = mutableListOf<DiffOp>()
    var current = node
    while (current?.prev != null) {
        val prev = current.prev
        val xDiff = current.x - prev.x
        val yDiff = current.y - prev.y
        when {
            // X, Y 모두 1씩 증가한 경우 대각선 이동, 즉 변경 없음.
            xDiff == 1 && yDiff == 1 -> {
                script.add(DiffOp.Keep(old[prev.x]))
            }
            // X만 1 증가한 경우 가로 이동, 즉 아이템 삭제.
            xDiff == 1 -> {
                script.add(DiffOp.Delete(old[prev.x]))
            }
            // Y만 1 증가한 경우 세로 이동, 즉 아이템 추가.
            yDiff == 1 -> {
                script.add(DiffOp.Insert(new[prev.y]))
            }
        }
        current = prev
    }
    // 역추적했으니 스크립트가 반대로 뒤집혀 있음. 뒤집어서 반환.
    return script.reversed()
}

Myeres’s Difference Algorithm의 성능 #

시간 복잡도 #

Myers’s Difference Algorithm의 시간 복잡도를 생각해보자.

우선 복잡도 계산에 필요한 주요 변수를 정의해야 한다. 알고리즘의 주요 사항은 두 리스트의 크기와 얼마나 두 리스트간의 차이가 있는가이다. 따라서 변수를 정의하자면 아래와 같이 할 수 있다.

  • \(N\): 이전 리스트의 크기.
  • \(M\): 최신 리스트의 크기.
  • \(D\): 편집 거리. 즉, 두 리스트의 차이점 크기. (두 리스트가 같으면 \(D = 0\), 완전히 다르면 \(D = N + M\))

우선 시간 복잡도는 \(O((N + M)D)\)이다. 공식을 보면 이 알고리즘의 시간 복잡도는 두 리스트가 얼마나 차이나냐에 따라서 크게 달라진다.

최선의 경우

두 리스트의 차이점이 없거나 매우 적은 경우를 생각해보자. 이 경우 \(D\)는 매우 작아지거나 0에 수렴한다. 단, 변경점이 아예 없더라도 최소한 리스트를 훑어보는 연산을 해야 한다. 따라서 리스트를 한번씩 훑어보는 것이 대부분의 연산이 되므로 복잡도는 \(O(N + M)\)에 수렴한다.

최악의 경우

만약 두 리스트가 매우 다르다면 \(D\)는 두 리스트의 합에 수렴한다 (\(D \approx N + M\)). 따라서 리스트를 한번씩 훑어보는 것에 더해 그만큼의 편집 거리 연산을 추가로 해야 하기 때문에 복잡도는 \(O((N + M)^2)\)이 된다.

공간 복잡도 #

Myers’s Difference Algotirhm은 두 리스트의 크기만큼의 행, 열을 가진 격자 위에서 이동하며 결과를 찾는 알고리즘이다. 하지만 위 구현에서 알 수 있듯이 알고리즘에서는 격자의 모든 영역을 활용하지 않고 현재 탐색 중인 각 대각선 경로에서 도달한 가장 깊은 \(x\) 좌표들의 배열만 사용한다. 따라서 \(N \times M\)만큼의 2차원 배열을 생성할 필요 없이 1차원 배열만 저장하며, 그 크기는 두 리스트의 크기의 합에 비례한다. 따라서 공간 복잡도는 \(O(N + M)\)이 된다.

만약 공간 복잡도가 \(O(NM)\)이였다면, 리스트의 아이템 개수가 늘어날수록 필요한 메모리의 양이 기하급수적으로 늘어난다. 특히 메모리가 적은 모바일 환경에서는 리스트가 커질수록 기기에 주는 부담이 너무 커졌을 것이다.

Myers’s Difference Algorithm의 한계와 DiffUtil의 해결법 #

Myeres’s Difference Algorithm은 최소한의 편집 작업을 구해낼 수 있지만 “추가”, “삭제”, “유지” 3가지 작업만 알 수 있다. 이 알고리즘을 그대로 리스트 UI에 적용하면 한 가지 문제가 발생한다. 바로 아이템의 이동을 삭제 후 추가로 인식한다는 것이다.

예를 들어 [A, B, C, D, E]와 [A, B, D, C, E] 리스트를 비교하면 아래와 같은 편집 스크립트가 나온다.

1: Keep   A
2: Keep   B
3: Delete C
4: Keep   D
5: Insert C
6: Keep   E

여기서는 먼저 C를 제거한 뒤 D를 유지하고 그 다음 C를 다시 추가해 자리 이동하라고 말한다. 하지만 리스트 UI에서 이런 동작을 실행하면 멀쩡히 있던 C가 사라진 후 D 뒤에서 다시 나타나는 애니메이션이 보인다. 애니메이션이 없더라도 이동한 부분의 UI 상태가 초기화될 수도 있다. 예를 들어 글자 입력이 가능한 TextField들의 리스트였다면 쓰고 있던 텍스트가 사라질 수도 있다.

DiffUtil에서는 약간의 추가 과정을 도입해서 “이동” 작업을 추가했다.

DiffUtil은 기존의 비교 동작 후에 2차 패스(Second Pass) 과정을 추가했다. 2차 패스는 비교를 통해 나온 최소 편집 스크립트(SES)에서 “삭제” 판정된 아이템과 “추가” 판정된 아이템들을 따로 모아 비교한다. 이 때, DiffUtil의 areItemsTheSame 메서드를 사용한다.

areItemsTheSame은 개발자가 직접 구현해 넘겨줘야 하는 메서드로, 리스트의 아이템의 고유성을 판단하는 메서드다. 두 개의 아이템이 실제로 같은 아이템인지 boolean 값을 반환하게 되어 있다. DiffUtil의 2차 패스 중에서 이 고유성을 비교해 “삭제” 판정된 아이템이 “추가"도 하도록 되어 있다면 “삭제”, “추가” 판정을 지우고 “이동” 판정으로 바꾼다.

마치며 #

지금까지 RecyclerView와 함께 자주 사용하던 DiffUtil의 핵심 알고리즘에 대해 알아보았다.

사실 Myers’s Difference Algorithm은 DiffUtil에서만 사용하는 알고리즘이 아니다. 이 알고리즘의 본질은 두 개의 시퀀스의 차이점을 최소한의 비용으로 찾아내는 것이 있고 여러 가지 비교 문제에 사용되고 있다. 예를 들면 Git은 두 개의 파일 변경 사항을 비교할 때 여러 가지 알고리즘을 지원하는데, 기본값으로 마이어스의 알고리즘을 사용한다. 우리가 개발하며 항상 봐온 git diff의 추가, 삭제 라인들은 사실 최소 편집 스크립트의 결과물이다.

또 DiffUtil이 알고리즘의 한계를 극복하기 위해 “아이템의 고유성"을 판단하는 아이디어는 UI 패러다임을 넘어서 널리 쓰이고 있다. RecyclerView와 Compose의 LazyList는 내부 구현이 다르지만 RecyclerView의 DiffUtil은 areItemsTheSame 메서드를 통해, LazyList는 key를 통해 아이템의 고유성을 판단하고 “삭제 후 추가” 대신 “이동"으로 치환한다는 점에서 같다.

결국 프레임워크나 라이브러리는 변하고 대체되지만 근본적인 원리나 아이디어는 그것을 넘어서 널리 사용된다. 항상 사용하는데 그치지 않고 그 원리를 이해한다면 엔지니어로 사는 동안 든든한 나의 자산이 되어줄 것이다.

  1. 시퀀스(Sequence)란, 순서가 있는 데이터의 나열이다. 여러 개의 문자가 나열된 문장이 될 수도 있고 숫자가 나열된 수열일 수도 있다. DiffUtil에서는 RecyclerView가 가진 데이터 List가 될 것이다. ↩︎

  2. 최단 편집 스크립트(Shortest Edit Script)란, 두 개의 시퀀스가 있을 때 하나의 시퀀스를 다른 하나의 시퀀스로 변환하기 위한 가장 적은 수의 편집을 하려면 어떤 명령을 해야 하는지의 집합이다. 즉, 가장 적은 편집으로 한 시퀀스를 다른 하나의 시퀀스로 변환하는 방법이다. ↩︎